Pratique | Débuter
L’ovale de Descartes permettrait de reproduire de façon universelle la forme des œufs des oiseaux

L’ovale de Descartes permet par exemple de reproduire la forme des œufs du Merle noir (Turdus merula).
Photographie : Przemek Pietrak / Wikimedia Commons
Introduction
Les œufs pondus par les oiseaux ont une grande diversité de couleurs et de motifs, même s’il n’existe que deux pigments à l’origine de leurs teintes, plus un autre responsable de la teinte rosée temporaire de ceux fraîchement pondus de certaines espèces, comme les pigeons et les tourterelles.
Ils peuvent avoir différentes formes (sphérique, elliptique, subelliptique, ovale, piriforme ou biconique), que la communauté scientifique essaie de décrire mathématiquement et de façon universelle depuis de nombreuses années. En 1948, le mathématicien allemand Fritz Hügelschäffer avait utilisé deux cercles non concentriques pour construire une ellipse déformée afin de former une courbe ovoïde, mais cette méthode ne permettait pas de représenter les œufs en forme de poire, ou piriformes : ce manque a été comblé récemment par des chercheurs qui ont fait évolué la formule initiale.
Dès le XVIIe siècle, dans le cadre de ses recherches en optique, le mathématicien, physicien et philosophe français René Descartes avait élaboré une courbe reliant tous les points fixes dont la moyenne pondérée des distances est constante. Cette représentation a été étudiée par d’autres mathématiciens au cours des siècles suivants, et Jean Lochet, un lecteur d’Ornithomedia.com, a constaté qu’elle permettait de reproduire la forme des œufs de nombreuses espèces.
Après un rappel général sur les différentes formes ovoïdes, nous évoquons l’étude publiée en 2021 proposant une adaptation de la formule de l’œuf de Fritz Hügelschäffer, puis nous présentons l’utilisation de l’ovale cartésien pour dessiner la forme d’une grande variété d’œufs.
Abstract
Bird eggs come in a wide variety of colors and patterns, although only two pigments give them their hues, plus another responsible for the temporary pinkish tint of newly laid eggs of some species, such as pigeons and turtledoves.
They can have various shapes (spherical, elliptical, subelliptical, oval, pear-shaped, or biconical), which the scientific community has been trying to describe mathematically and universally for many years. In 1948, German mathematician Fritz Hügelschäffer used two non-concentric circles to construct a deformed ellipse to form an ovoid curve, but this method failed to represent pear-shaped, or pear-shaped, eggs: this shortcoming has recently been addressed by researchers who have evolved the original formula. As early as the 17th century, as part of his research in optics, the French mathematician, physicist, and philosopher René Descartes developed a curve connecting all fixed points whose weighted average distances are constant. This representation was studied by other mathematicians over the following centuries, and Jean Lochet, an Ornithomedia.com reader noted that it would make it possible to accurately reproduce the eggs of many species.
After a general overview of the different egg shapes, we discuss the study published in 2021 proposing an adaptation of Fritz Hügelschäffer’s egg formula, and then we present the use of the Cartesian oval to represent a wide variety of eggs.
Les différentes formes d’œufs d’oiseaux
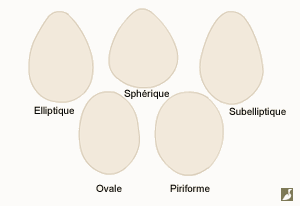
Les différentes formes d’œufs (la forme biconique, très rare, n’est pas illustrée). |
Au printemps, il est fréquent de trouver dans son jardin, dans un parc ou dans un bâtiment des nids dans lesquels des œufs ont été pondus, mais si les parents ne sont pas visibles, il n’est pas toujours simple de savoir de quelle espèce il s’agit. Pour identifier l’espèce, il faut prendre en compte différents facteurs : l’habitat (forêt, marais, etc.), la forme (plateforme, coupe, etc.), l’emplacement (dans un arbre, au sol, etc.) et les matériaux (brindilles, mousses, etc.) du nid, mais aussi l’aspect, les couleurs, les dimensions et la forme des œufs (lire Identifier les nids et les œufs des oiseaux des villes et des jardins).
Il existe différentes formes :
- sphérique : proche de la forme d’une sphère.
- Elliptique : allongé, plus large en son milieu, avec des extrémités également arrondies.
- Subelliptique : arrondi aux extrémités, plus allongé que le précédent, s’amincissant aux extrémités dont l’une est plus large que l’autre.
- Ovale : la forme typique, avec une extrémité plus large et plus arrondie, l’autre étant relativement pointue.
- Piriforme : en forme de poire.
- Biconique : pointu aux deux extrémités (grèbes).
Une formule mathématique universelle permettant de reproduire les différentes formes ovoïdes
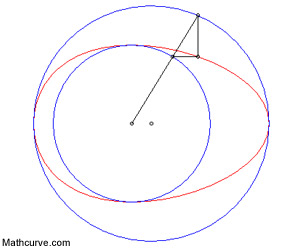
L’œuf de Hügelschäffer (courbe rouge). |
Depuis longtemps, des mathématiciens essaient de mettre au point une formule permettant de représenter les œufs de toutes les espèces d’oiseaux. Cette recherche, qui semble d’une importance toute relative, présente toutefois de nombreux intérêts, allant d’une meilleure compréhension de l’évolution de la classe Aves (qui regroupe les vertébrés tétrapodes ailés) depuis le Jurassique (lire L’évolution des oiseaux au Jurassique et au Crétacé), à la conception d’emballages efficaces, en passant par la conception de formes ovoïdes permettant de supporter des charges maximales.
En 1948, le mathématicien allemand Fritz Hügelschäffer avait utilisé une méthode de Newton basée sur deux cercles non concentriques (= dont les repères sont distincts) pour construire une ellipse déformée afin de former une courbe ovoïde. Lorsque leurs centres sont confondus, on obtient la construction classique d’une ellipse, et quand on les décale, on supprime la symétrie et on produit une courbe ovoïde.
Toutefois, cette approche ne permet pas de reproduire les œufs piriformes (= en forme de poire). Dans un article paru en août 2021 dans la revue Annals of the New York Academy of Sciences, les auteurs ont proposé une nouvelle formule mathématique basée sur une évolution de la transformation de Fritz Hügelschäffer et qui s’applique à tous les types d’œufs. Pour y parvenir, ils ont utilisé les dimensions fondamentales de l’œuf (longueur, largeur maximale et diamètre au quart de sa longueur) et ont introduit une fonction supplémentaire, à savoir le décalage de son axe vertical. En intégrant ces valeurs, faciles à mesurer avec des instruments de mesure classique, ils ont réussi à établir une nouvelle équation.
Une courbe plus ancienne, l’ovale cartésien, permettrait aussi de représenter toutes les formes ovoïdes
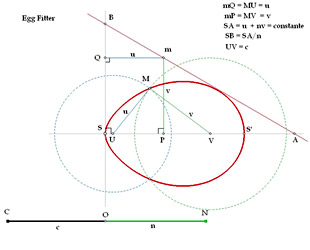
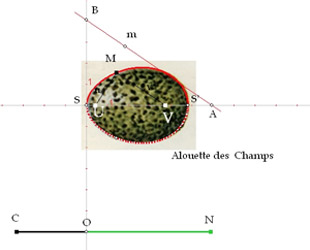
Schéma 1 – Description géométrique d’un ovale de Descartes (courbe rouge) (cliquez sur le schéma pour l’agrandir). |
L’ovale cartésien a été imaginé au XVIIe siècle par René Descartes, initialement pour ses recherches en optique sur la réfraction : il avait alors remplacé une sphère ronde en verre éclairé par un faisceau de rayons parallèles (venant du soleil par exemple) par une de forme ovoïde pour assurer un point parfait de convergence.
L’ovale de Descartes correspond à l’ensemble des points dont la moyenne pondérée des distances est constante. On utilise pour cela deux cercles, de centre U et de rayon u = mQ et de centre V et de rayon v = mP, qui se croisent en un point M (voir le schéma 1 ci-dessous) : lorsque le point m décrit une ligne AB, le point M décrit la courbe en rouge, que l’on appelle ovale de Descartes. Elle est définie par le fait que MU + nMV (avec n = SA/SB) reste constant, quelle que soit la position de M sur l’ovale : on obtient par exemple une ellipse quand n = 1.
La méthode du jardinier, qui permet de créer un parterre de forme ovale, est une application pratique de l’ovale de Descartes : elle consiste à planter deux piquets, à attacher une ficelle mal tendue de l’un à l’autre, puis à utiliser un troisième piquet pour tendre le fil et tracer une ellipse sur le sol avec ce dernier piquet. Toutefois, le jardinier ne pourra tracer ainsi qu’une demi-ellipse : au-delà, la ficelle va en effet s’enrouler autour de l’un des piquets plantés, et il devra donc s’y prendre à deux fois (voir une vidéo).
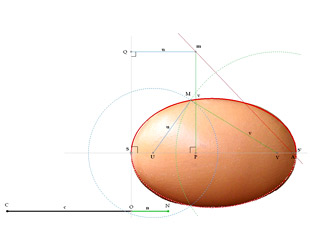
En se basant sur la méthode de l’ovale cartésien, on peut élaborer, avec un logiciel simple de mathématiques et de géométrie dynamiques, comme Cabri II Plus de la société Cabrilog, ou Geogebra, un algorithme itératif pour reproduire la forme des œufs de nombreuses espèces : il suffit de faire coïncider leur plus grand axe avec les points S et S’, puis à l’aide des curseurs OC et ON, d’ajuste au mieux leur contour (voir le schéma 2 et la vidéo ci-dessous).
Jean Lochet, le lecteur d’Ornithomedia.com qui a fait ce constat a pu vérifier que cette méthode fonctionnait avec des oiseaux très variés (limicoles, rapaces, passereaux, gallinacés, rallidés, etc.) et des formes différentes, y compris piriforme comme celui du Guillemot de Troïl (Uria aalge). Ses tests ne sont toutefois certainement pas exhaustifs, et il faudrait s’assurer que toutes les formes possibles sont bien reproductibles :
La possibilité de pouvoir représenter de façon mathématique tous les œufs, quelle que soit leur forme, est remarquable, mais elle n’est pas encore explicable : s’agit-il d’un simple hasard ou du résultat de règles biologiques encore inconnues ?
Vidéo montrant comment utiliser un ovale cartésien pour représenter un œuf
Utiliser un ovale cartésien pour représenter un œuf : il suffit de faire coïncider son grand axe avec les points S et S’, puis à l’aide des curseurs OC et ON, d’ajuster au mieux sa forme.
Source : chaîne YouTube d’Ornithomedia.com
Réagir à notre article
Compléments
Ouvrages recommandés
- Nids et oeufs de Maurice Dupérat
- Le nid, l’oeuf et l’oiseau de David Burnie et Véronique Dreyfus
Sources
- Ives Etienne (2024). Mathématiques : une équation universelle existe pour décrire la forme de l’œuf . Sciences et Vie. Date : 02/06. www.science-et-vie.com
- Pierre Audin et Guilaume Reuiller (2006). Comment agrandir une ellipse ? Palais de la Découverte. Numéro : 332. www.palais-decouverte.fr
- Mathcurve. Ovale de Descartes. www.mathcurve.com
- Mathcurve. oeuf de Hügelschaäffer. www.mathcurve.com









Aucun commentaire sur ce sujet
Participer à la discussion !